Fast Romano-Wolf Multiple Testing Corrections for fixest 🐺
For the final chapter of my dissertation, I had examined the effects of ordinal class rank on the academic achievement of Danish primary school students (following a popular identification strategy introduced in a paper by Murphy and Weinhard). Because of the richness of the Danish register data, I had a large number of potential outcome variables at my disposal, and as a result, I was able to examine literally all the outcomes that the previous literature had covered in individual studies - the effect of rank on achievement, personality, risky behaviour, mental health, parental investment, etc. - in one paper.
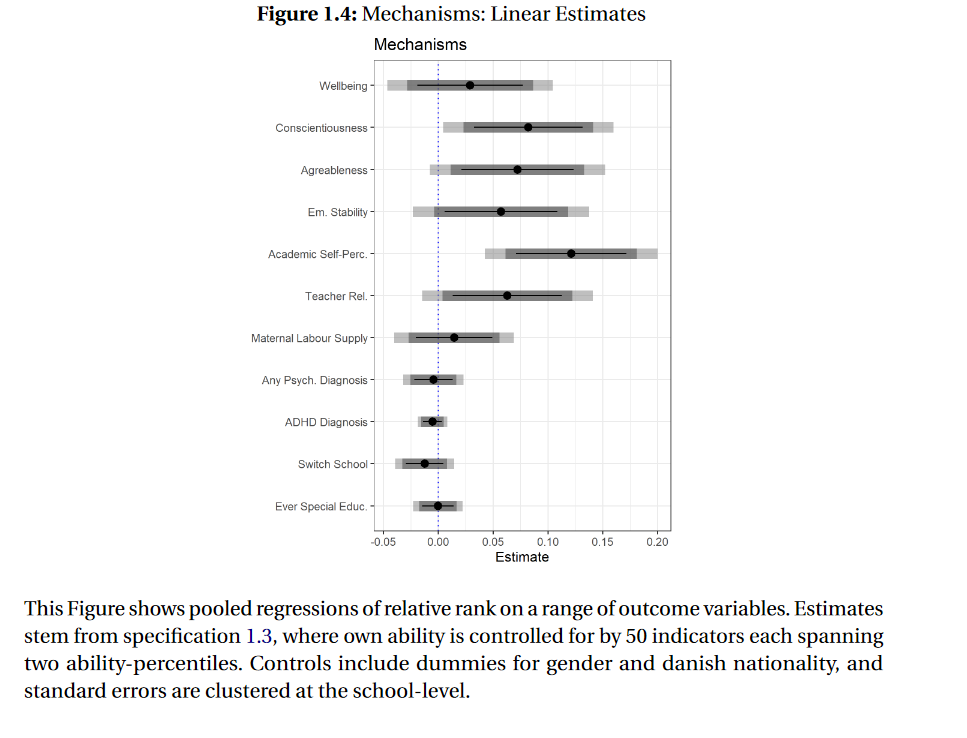
Figure 1: The Effect of Ordinal Class Rank on quite a few outcome variables
But with (too) many outcome variables comes a risk: inflated type 1 error rates, or an increased risk of ‘false positives’. So I was wondering: were all the significant effects I estimated - shown in the figure above - “real”, or was I simply being fooled by randomness?
A common way to control the risk of false positive when testing multiple hypothesis is to use methods that control the ‘family-wise’ error rate, i.e. the risk of at least one false positive in a family of S hypotheses.
Among such methods, Romano and Wolf’s correction is particularly popular, because it is “uniformly the most powerful”. Without going into too much detail, I’ll just say that if you have a choice between a number of methods that control the family-wise error rate at a desired level \(\alpha\), you might want to choose the “most powerful” one, i.e. the one that has the highest success rate of finding a true effect.
Now, there is actually an amazing Stata package for the Romano-Wolf method called rwolf.
But this is an R blog, and I’m an R guy … In addition, my regression involved several million rows and some high-dimensional fixed effects, and rwolf quickly showed its limitations. It just wasn’t fast enough!
While playing around with the rwolf package, I finally did my due diligence on the method it implements, and after a little background reading, I realized that both the Romano and Wolf method - as well as its main rival, the method proposed by Westfall and Young - are based on the bootstrap!
But wait! Had I not just spent a lot of time porting a super-fast bootstrap algorithm from R to Stata? Could I not use Roodman et al’s “fast and wild” cluster bootstrap algorithm for bootstrap-based multiple hypothesis correction?
Of course it was inevitable: I ended up writing an R package. Today I am happy to present the first MVP version of the wildwrwolf package!
The wildrwolf package
You can simply install the package from github or r-universe by typing
# install.packages("devtools")
devtools::install_github("s3alfisc/wildrwolf")
# from r-universe (windows & mac, compiled R > 4.0 required)
install.packages('wildrwolf', repos ='https://s3alfisc.r-universe.dev')The Romano Wolf correction in wildrwolf is implemented as a post-estimation commands for multiple estimation objects from the fabulous fixest package.
To demonstrate how wildrwolf's main function, rwolf, works, let’s first simulate some data:
library(wildrwolf)
library(fixest)
set.seed(1412)
library(wildrwolf)
library(fixest)
set.seed(1412)
N <- 5000
X1 <- rnorm(N)
X2 <- rnorm(N)
rho <- 0.5
sigma <- matrix(rho, 4, 4); diag(sigma) <- 1
u <- MASS::mvrnorm(n = N, mu = rep(0, 4), Sigma = sigma)
Y1 <- 1 + 1 * X1 + X2
Y2 <- 1 + 0.01 * X1 + X2
Y3 <- 1 + 0.4 * X1 + X2
Y4 <- 1 + -0.02 * X1 + X2
for(x in 1:4){
var_char <- paste0("Y", x)
assign(var_char, get(var_char) + u[,x])
}
group_id <- sample(1:100, N, TRUE)
data <- data.frame(Y1 = Y1,
Y2 = Y2,
Y3 = Y3,
Y4 = Y4,
X1 = X1,
X2 = X2,
group_id = group_id,
splitvar = sample(1:2, N, TRUE))We now estimate a regression via the fixest package:
fit <- feols(c(Y1, Y2, Y3, Y4) ~ csw(X1,X2),
data = data,
cluster = ~group_id,
ssc = ssc(cluster.adj = TRUE))
# clean workspace except for res & data
rm(list= ls()[!(ls() %in% c('fit','data'))])For all eight estimated regressions, we want to apply the Romano-Wolf correction to the parameter of interest, X1. We simply need to provide the regression object of type fixest_multi (it is also possible to simply provide a list of objects of type fixest), the parameter of interest, the number of bootstrap draws, and possibly a seed (for replicability). That’s it! If the regressions use clustered standard errors, rwolf will pick this up and run a wild cluster bootstrap, otherwise just a robust wild bootstrap.
pracma::tic()
res_rwolf <- wildrwolf::rwolf(
models = fit,
param = "X1",
B = 9999,
seed = 23
)##
|
| | 0%
|
|========= | 12%
|
|================== | 25%
|
|========================== | 38%
|
|=================================== | 50%
|
|============================================ | 62%
|
|==================================================== | 75%
|
|============================================================= | 88%
|
|======================================================================| 100%pracma::toc()## elapsed time is 3.980000 secondsFor \(N=5000\) observations with \(G=100\) clusters, \(S=8\) hypothesis and \(B=9999\) bootstrap draws, the calculation of Romano-Wolf corrected p-values takes less than 5 seconds. If you ask me, that is pretty fast! =) 🚀
We can now compare the results of rwolf with the uncorrected p-values and another popular multiple testing adjustment, Holm’s method.
pvals <- lapply(fit, function(x) pvalue(x)["X1"]) |> unlist()
df <-
data.frame(
"uncorrected" = pvals,
"Holm" = p.adjust(pvals, method = "holm"),
"rwolf" = res_rwolf$pval
)
rownames(df) <- NULL
round(df, 3)## uncorrected Holm rwolf
## 1 0.000 0.000 0.000
## 2 0.000 0.000 0.000
## 3 0.140 0.420 0.367
## 4 0.033 0.132 0.128
## 5 0.000 0.000 0.000
## 6 0.000 0.000 0.000
## 7 0.398 0.420 0.394
## 8 0.152 0.420 0.367Both Holm’s method and rwolf produce similar corrected p-values, which - in general - are larger than the uncorrected p-values.
But does it actually work? Monte Carlo Experiments
We test \(S=6\) hypotheses and generate data as
\[Y_{i,s,g} = \beta_{0} + \beta_{1,s} D_{i} + u_{i,g} + \epsilon_{i,s} \] where \(D_i = 1(U_i > 0.5)\) and \(U_i\) is drawn from a uniform distribution, \(u_{i,g}\) is a cluster level shock with intra-cluster correlation \(0.5\), and the idiosyncratic error term is drawn from a multivariate random normal distribution with mean \(0_S\) and covariance matrix
S <- 6
rho <- 0.5
Sigma <- matrix(1, 6, 6)
diag(Sigma) <- rho
SigmaThis experiment imposes a data generating process as in equation (9) in Clarke, Romano and Wolf, with an additional error term \(u_g\) for \(G=20\) clusters and intra-cluster correlation 0.5 and \(N=1000\) observations.
You can run the simulations via the run_fwer_sim() function attached
in the package.
# note that this will take some time
res <- run_fwer_sim(
seed = 232123,
n_sims = 500,
B = 499,
N = 1000,
s = 6,
rho = 0.5 #correlation between hypotheses, not intra-cluster!
)
# > res
# reject_5 reject_10 rho
# fit_pvalue 0.274 0.460 0.5
# fit_pvalue_holm 0.046 0.112 0.5
# fit_padjust_rw 0.052 0.110 0.5Both Holm’s method and wildrwolf control the family wise error rates, at both the 5 and 10% significance level. Very cool!
The method by Westfall and Young
A package for Westfall and Young’s (1993) method is currently in development. I am not yet fully convinced that it works as intented - in simulations, I regularly find that wildwyoung overrejects.
Literature
Clarke, Damian, Joseph P. Romano, and Michael Wolf. “The Romano–Wolf multiple-hypothesis correction in Stata.” The Stata Journal 20.4 (2020): 812-843.
Murphy, Richard, and Felix Weinhardt. “Top of the class: The importance of ordinal rank.” The Review of Economic Studies 87.6 (2020): 2777-2826.
Romano, Joseph P., and Michael Wolf. “Stepwise multiple testing as formalized data snooping.” Econometrica 73.4 (2005): 1237-1282.
Roodman, David, et al. “Fast and wild: Bootstrap inference in Stata using boottest.” The Stata Journal 19.1 (2019): 4-60.
Westfall, Peter H., and S. Stanley Young. Resampling-based multiple testing: Examples and methods for p-value adjustment. Vol. 279. John Wiley & Sons, 1993.