Fast wild cluster bootstrap inference

boottest is a S3 method that allows for fast wild cluster bootstrap inference for objects of class lm, fixest and felm by implementing the fast wild bootstrap algorithm developed in Roodman et al., 2019.

Usage

boottest(object, ...)

Arguments

object: An object of type lm, fixest, felm or ivreg
...: other arguments

Value

An object of class boottest.

Details

Technical Details For technical details, either take a look at the references below, or check out the wild (cluster) bootstrap vignette.

Setting Seeds

To guarantee reproducibility, you can either use boottest()'s seed function argument, or set a global random seed via

set.seed() when using
1. the lean algorithm (via engine = "R-lean"), 2) the heteroskedastic wild bootstrap
2. the wild cluster bootstrap via engine = "R" with Mammen weights or 4) engine = "WildBootTests.jl"
dqrng::dqset.seed() when using engine = "R" for Rademacher, Webb or Normal weights

Stata, Julia and Python Implementations

The fast wild cluster bootstrap algorithms are further implemented in the following software packages:

References

Roodman et al., 2019, "Fast and wild: Bootstrap inference in STATA using boottest", The STATA Journal. (https://ideas.repec.org/p/qed/wpaper/1406.html)

MacKinnon, James G., Morten Ørregaard Nielsen, and Matthew D. Webb. Fast and reliable jackknife and bootstrap methods for cluster-robust inference. No. 1485. 2022.

Cameron, A. Colin, Jonah B. Gelbach, and Douglas L. Miller. "Bootstrap-based improvements for inference with clustered errors." The Review of Economics and Statistics 90.3 (2008): 414-427.

Cameron, A.Colin & Douglas L. Miller. "A practitioner's guide to cluster-robust inference" Journal of Human Resources (2015) doi:10.3368/jhr.50.2.317

Davidson & MacKinnon. "Wild Bootstrap Tests for IV regression" Journal of Economics and Business Statistics (2010) doi:10.1198/jbes.2009.07221

MacKinnon, James G., and Matthew D. Webb. "The wild bootstrap for few (treated) clusters." The Econometrics Journal 21.2 (2018): 114-135.

MacKinnon, James G., and Matthew D. Webb. "Cluster-robust inference: A guide to empirical practice" Journal of Econometrics (2022) doi:10.1016/j.jeconom.2022.04.001

MacKinnon, James. "Wild cluster bootstrap confidence intervals." L'Actualite economique 91.1-2 (2015): 11-33.

Webb, Matthew D. "Reworking wild bootstrap based inference for clustered errors" . No. 1315. Queen's Economics Department Working Paper, 2013.

Examples

requireNamespace("fwildclusterboot")
data(voters)
lm_fit <- lm(
  proposition_vote ~ treatment + ideology1 + log_income + Q1_immigration,
  data = voters
)
boot <- boottest(lm_fit,
  B = 9999,
  param = "treatment",
  clustid = "group_id1"
)
#> Warning: Please note that the seeding behavior for random number generation for
#> `boottest()` has changed with `fwildclusterboot` version 0.13.
#> 
#> It will no longer be possible to exactly reproduce results produced by versions
#> lower than 0.13.
#> 
#> If your prior results were produced under sufficiently many bootstrap
#> iterations, none of your conclusions will change. For more details about this
#> change, please read the notes in
#> [news.md](https://cran.r-project.org/web/packages/fwildclusterboot/news/news.html).
#> This warning is displayed once per session.
#> Too guarantee reproducibility, don't forget to set a global random seed
#> **both** via `set.seed()` and `dqrng::dqset.seed()`.
#> This message is displayed once every 8 hours.
summary(boot)
#> boottest.lm(object = lm_fit, param = "treatment", B = 9999, clustid = "group_id1")
#> 	
#>  Hypothesis: 1*treatment = 0
#>  Observations: 300
#>   Bootstr. Type: rademacher
#>  Clustering: 1-way
#>  Confidence Sets: 95%
#>  Number of Clusters: 40
#>  
#>              term estimate statistic p.value conf.low conf.high
#> 1 1*treatment = 0    0.073     3.709   0.001    0.034     0.113
print(boot)
#> boottest.lm(object = lm_fit, param = "treatment", B = 9999, clustid = "group_id1")
#>  
#> p value: 9e-04 
#> confidence interval: 0.0336 0.1129 
#> test statistic 3.7094 
plot(boot)

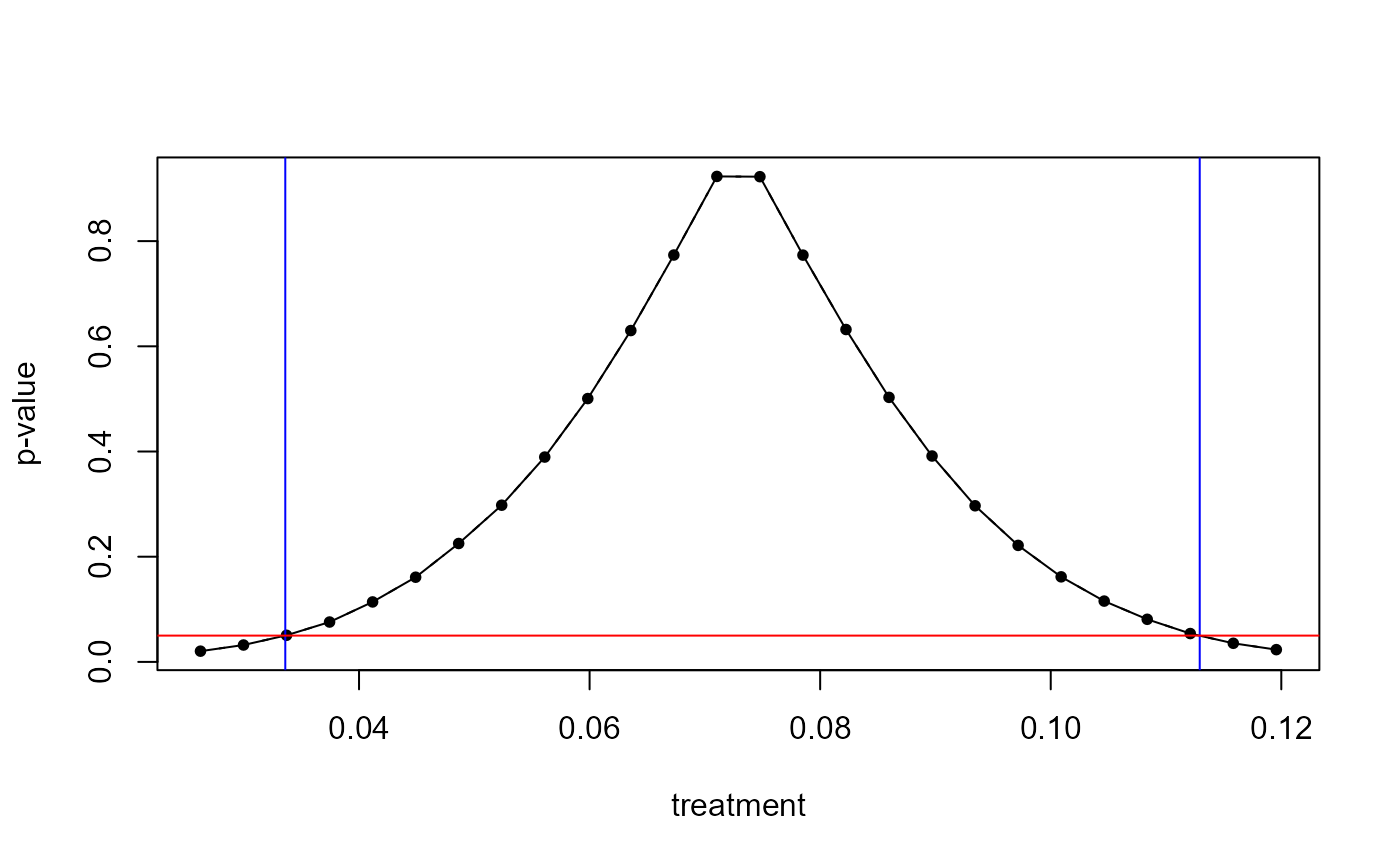nobs(boot)
#> [1] 300
pval(boot)
#> [1] 0.00090009
confint(boot)
#> [1] 0.0336039 0.1129239
generics::tidy(boot)
#>              term   estimate statistic    p.value  conf.low conf.high
#> 1 1*treatment = 0 0.07290769  3.709435 0.00090009 0.0336039 0.1129239